Câu hỏi:
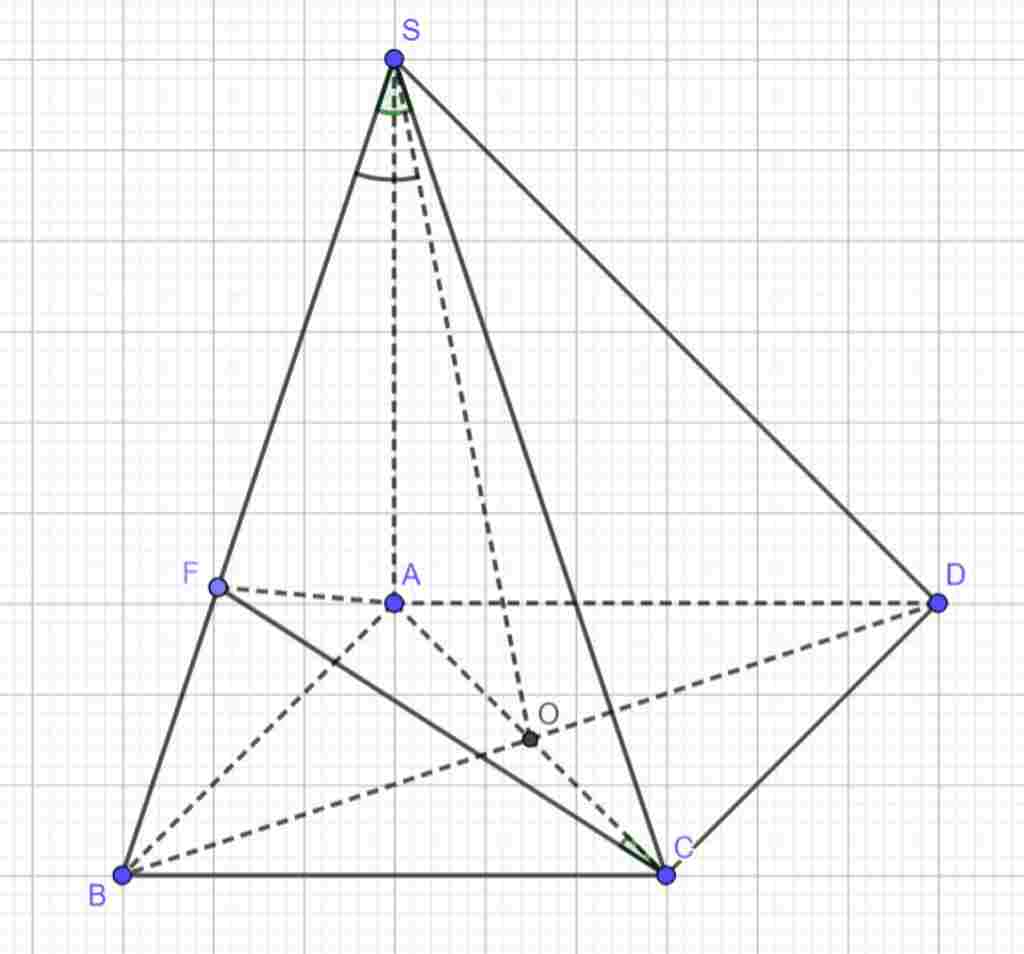
Giúp em bài tập về nhà Toán lớp 11 câu hỏi như sau: hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mp đáy, SA=a √6. Tính góc giữa
a)SC và (SAB)
b)SB và (SAC)
c)AC và (SBC)
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:

Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Ta có:
$\left\{\begin{array}{I}CB\bot AB\\CB\bot SA\end{array}\right.\Rightarrow CB\bot (SAB)$
$\Rightarrow B$ là hình chiếu của $C$ lên $(SAB)$
$\Rightarrow(SC,(SAB))=(SC,SB)=\widehat{CSB}$
Từ $CB\bot (SAB)\Rightarrow CB\bot SB$
$\Delta SBC\bot B$ có $BC=a, SB=\sqrt{AB^2+SA^2}=a\sqrt7$
$\tan\widehat{CSB}=\dfrac{BC}{SB}=\dfrac{a}{a\sqrt7}=\dfrac1{\sqrt7}$
$\Rightarrow (SC,(SAB))=\widehat{CSB}=\arctan\dfrac1{\sqrt7}≈20,7^o$
b) Ta có:
$\left\{\begin{array}{I}BD\bot AC\\BD\bot SA\end{array}\right.\Rightarrow BD\bot (SAC)$
Gọi $O=AC\cap BD$
$\Rightarrow O$ là hình chiếu của $B$ lên $(SAC)$
$\Rightarrow(SB,(SAC))=(SB,SO)=\widehat{BSO}$
Ta có $BD\bot (SAC)$ (chứng minh trên) $\Rightarrow BO\bot SO$
$\Delta BSO\bot O$ có $BO=\dfrac a{\sqrt2},SB=a\sqrt7$
$\Rightarrow\sin\widehat{BSO}=\dfrac{BO}{SB}=\dfrac{1}{\sqrt{14}}$
$\Rightarrow(SB,(SAC))=\widehat{BSO}=\arcsin\dfrac{1}{\sqrt{14}}≈15,5^o$
c) Tam giac $SAB$ dựng $AF\bot SB$
Ta có $BC\bot(SAB)$ (chứng minh trên) nên $BC\bot AF$
$\Rightarrow AF\bot(SBC)$
Suy ra F là hình chiếu của A lên $(SBC)$
$\Rightarrow (AC,(SBC))=(AC,FC)=\widehat{ACF}$
Từ $AF\bot(SBC)\Rightarrow AF\bot CF$
$\Rightarrow\Delta ACF\bot F$ có $AC= a\sqrt2$
$\Delta SAB:\dfrac{1}{AF^2}=\dfrac{1}{AS^2}+\dfrac1{AB^2}$
$\Rightarrow AF=\dfrac{a\sqrt6}{\sqrt7}$
$\Rightarrow \sin\widehat{ACF}=\dfrac{AF}{AC}=\dfrac{\sqrt{3}}{\sqrt7}$
$\Rightarrow(AC,(SBC))=\widehat{ACF}=\arcsin\dfrac{\sqrt{3}}{\sqrt7}≈40,89^o$.