Câu hỏi:
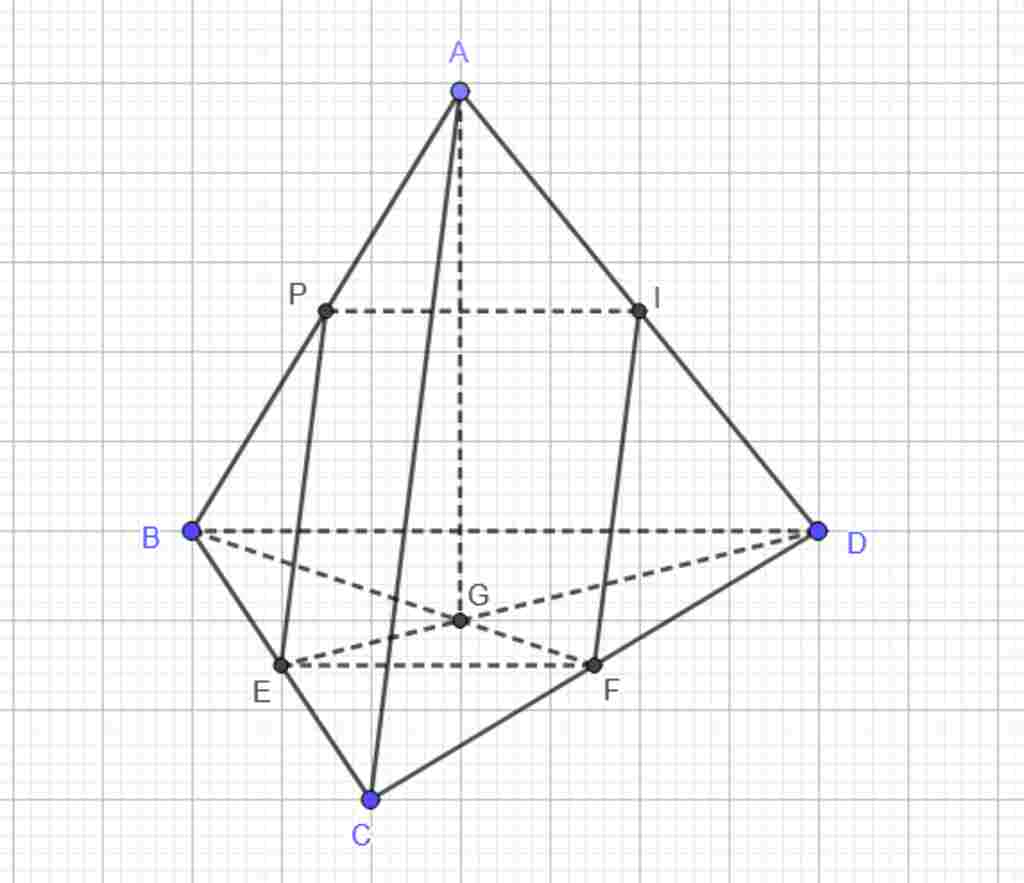
Giúp em bài tập về nhà Toán lớp 11 câu hỏi như sau: Cho tứ diện ABCD có AB=AC=AD=24, BC=CD=DB=15. Trên cạnh AB lấy điểm P sao cho PA=xPB. Với giá trị nào của x thì mặt phẳng (a) qua P song song với AC và BD cắt tứ diện ABCD theo thiết diện là một hình thoi?
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
$x=\dfrac{24}{15}$
Lời giải và giải thích chi tiết:
$PA=xPB\Rightarrow\dfrac{PA}{PB}=x$
$\Rightarrow\dfrac{PA}{PB+PA}=\dfrac{x}{1+x}\Rightarrow \dfrac{PA}{AB}=\dfrac{x}{x+1}$ và
$\dfrac{BP}{PA+PB}=\dfrac{1}{x+1}\Rightarrow \dfrac{PB}{AB}=\dfrac{1}{x+1}$
$\Delta ABD$ dựng $PI//BD\Rightarrow\dfrac{PI}{BD}=\dfrac{AP}{AB}$
$\Delta ABC$ dựng $PE//AC\Rightarrow \dfrac{PE}{AC}=\dfrac{BP}{BA}$
$\Rightarrow (PIE)$ chính là $(a)$, dựng $IF//AC\Rightarrow PIFE$ là thiết diện của hình chóp $(ABCD)$ cắt bởi $(a)$
Do $IF//=PE$ nên $PIFE$ là hình bình hành để tứ giác là hình thoi thì $PI=PE$
mà $PI=\dfrac{AP}{AB}.BD=\dfrac{x}{x+1}.15$
$PE=\dfrac{BP}{BA}.AC=\dfrac{1}{x+1}.24$
$PI=PE\Rightarrow 15x=24\Rightarrow x=\dfrac{24}{15}$.