Câu hỏi:
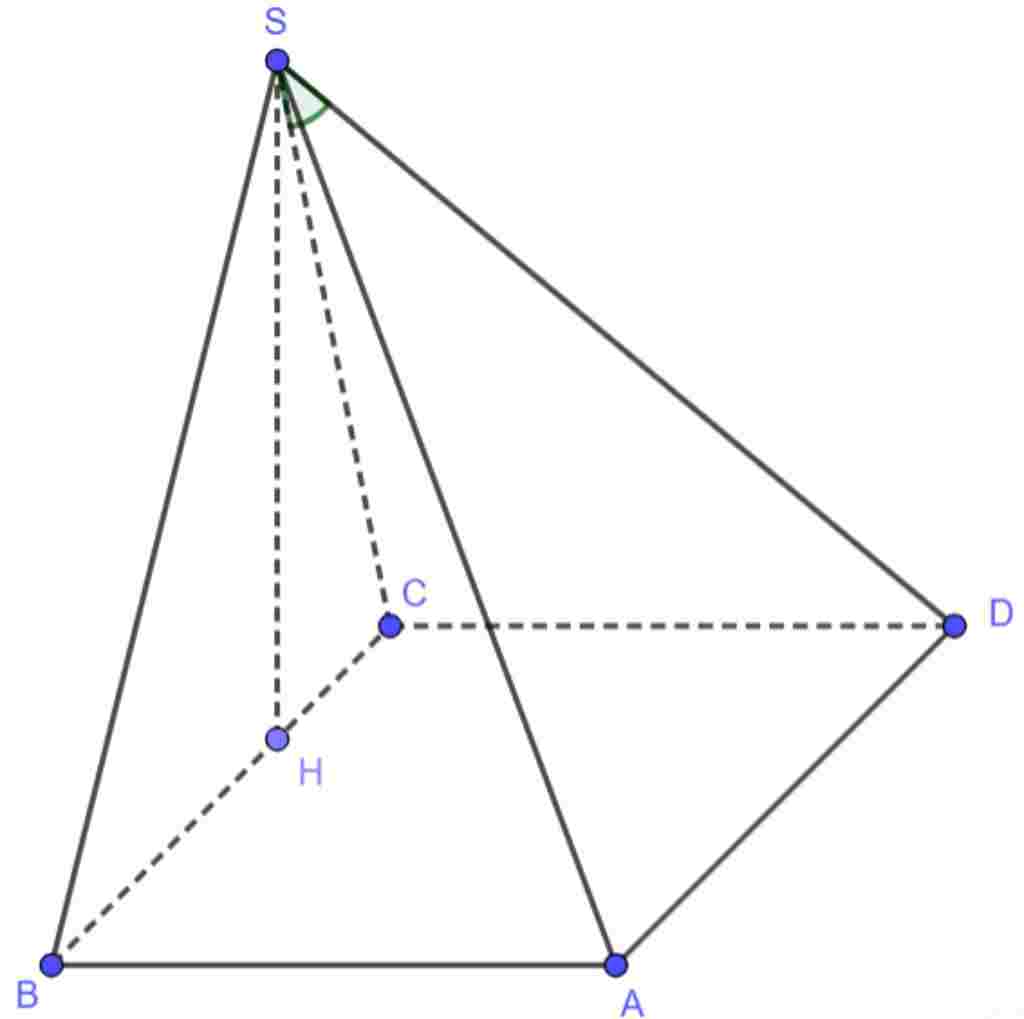
Giúp em bài tập về nhà Toán lớp 11 câu hỏi như sau: cho hình chóp s.abcd có đáy abcd là hình vuông cạnh √3 , tam giác sbc vuông tại s và nằm trong mặt phẳng vuông góc với đáy , đường thẳng sd tạo với mặt phẳng (sbc) một góc 60 độ. tính thể tích v của khối chóp s.abcd . Help meeeeeeeeeeee , toán hình xem mà chẳng hỉu gì cả nên lên đây nhờ cao nhân giúp với :3
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
$V_{SABCD}=\dfrac{\sqrt6}3$
Lời giải:
Do $\Delta SBC\bot S$ nằm trong mặt phẳng vuông góc với đáy, $(SBC)\bot(ABCD)$
$\Delta SBC$ dựng $SH\bot BC\Rightarrow SH\bot(ABCD)$
Ta có:
$DC\bot BC$ (do tứ giác ABCD là hình vuông)
$DC\bot SH$ (do $SH\bot (ABCD)$ chứng minh trên)
mà $BC, SH\in(SBC)\Rightarrow DC\bot(SBC)\Rightarrow DC\bot SC$
và $\Rightarrow\widehat{(SD,(SBC))}=(SD,SC)=\widehat{CSD}=60^o$
$\Delta SCD\bot C$:
$\tan\widehat{CSD}=\dfrac{CD}{SC}$
$\Rightarrow SC=\dfrac{CD}{\tan\widehat{CSD}}=1$
$\Delta SBC\bot S, SH\bot BC$
$SB^2=BC^2-SC^2=\sqrt2$
$\dfrac1{SH^2}=\dfrac1{SB^2}+\dfrac1{SC^2}=\dfrac32$
$\Rightarrow SH=\dfrac{\sqrt2}{\sqrt3}$
$\Rightarrow V_{SABCD}=\dfrac13.SH.S_{ABCD}$
$=\dfrac13.\dfrac{\sqrt2}{\sqrt3}.\sqrt3.\sqrt3=\dfrac{\sqrt2}{\sqrt3}=\dfrac{\sqrt6}3$
