Câu hỏi:
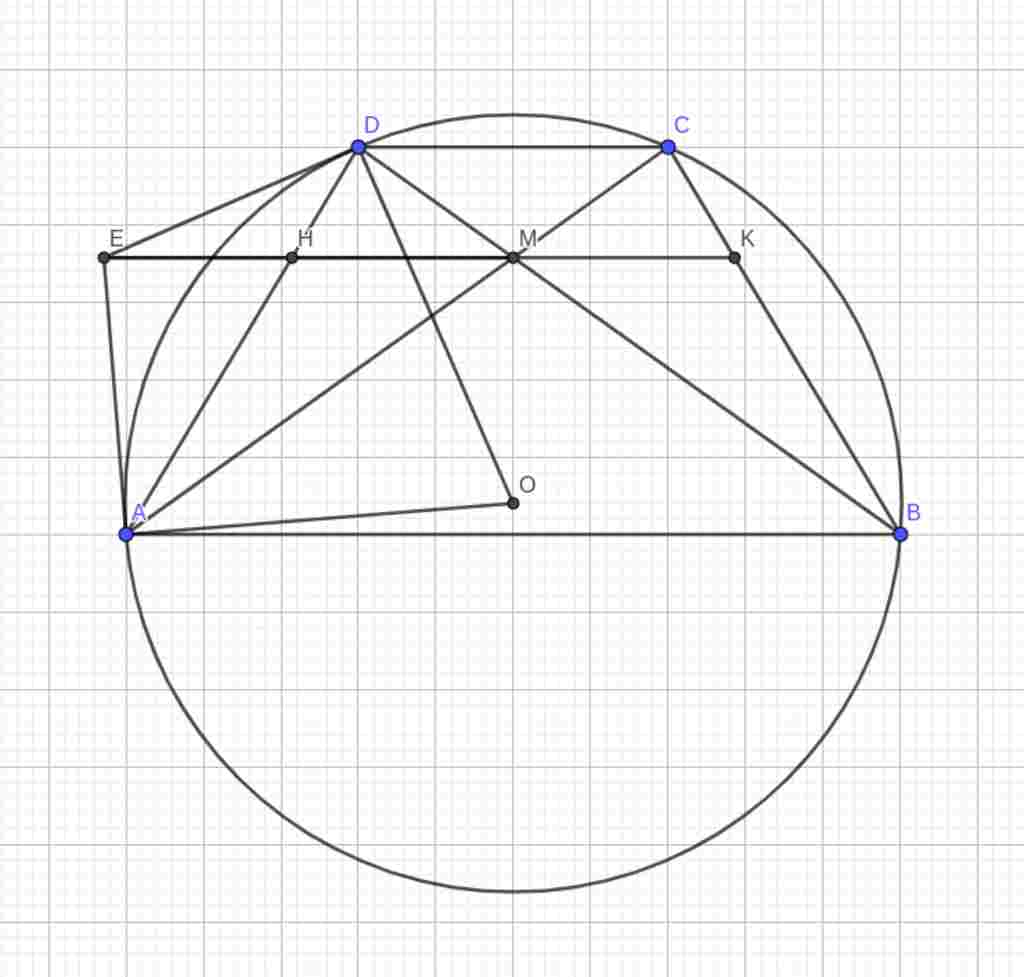
Giúp em bài tập về nhà Toán lớp 10 câu hỏi như sau: Cho hình thang cân ABCD (AB > CD, AB // CD) nội tiếp trong đường tròn (O). Kẻ các tiếp tuyến với đường tròn (O) tại A và D chúng cắt nhau ở E. Gọi M là giao điểm của hai đường chéo AC và BD.
1. Chứng minh tứ giác AEDM nội tiếp được trong một đường tròn.
2. Chứng minh AB // EM.
3. Đường thẳng EM cắt cạnh bên AD và BC của hình thang lần lượt ở H và K. Chứng minh M là trung điểm HK.
4. Chứng minh:
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
1. Ta có:
$ED,EA$ là tiếp tuyến của (O)
$\to ED\perp OD, EA\perp OA\Rightarrow\widehat{ADE}=\widehat{OAE}=90^o$
$EDOA$ có $\widehat{ADE}+\widehat{OAE}=180^o$
$\Rightarrow EDOA$ nội tiếp đường tròn đường kính (OE)
$\to \widehat{DOA}+\widehat{DEA}=180^o$
Mà $ABCD$ là hình thang cân
$\to\widehat{DMA}=\widehat{DBA}+\widehat{CAB}=2\widehat{DBA}=\widehat{DOA}$
$\to \widehat{DMA}+\widehat{AED}=180^o\to AEDM$ nội tiếp được trong một đường tròn
2. Từ câu 1
$\to\widehat{EMA}=\widehat{EDA}=\widehat{DBA}=\widehat{CAB}$
Vì $ED$ là tiếp tuyến của (O),$ABCD$ là hình thang cân
$\to EM//AB$
3. Ta có:
$EM//AB\to HK//AB\to\dfrac{HM}{AB}=\dfrac{DM}{DB}=\dfrac{CM}{CA}=\dfrac{MK}{AB}$
$\to MH=MK\to M$ là trung điểm HK