Câu hỏi:
Giúp em bài tập về nhà Toán lớp 10 câu hỏi như sau: cho tam giác ABC vuông tại A và AB = 3, AC = 4. Tính độ dài vecto CB + vecto AB.
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
$|\vec{CB}+\vec{AB}|=2\sqrt{13}$
Lời giải và giải thích chi tiết:
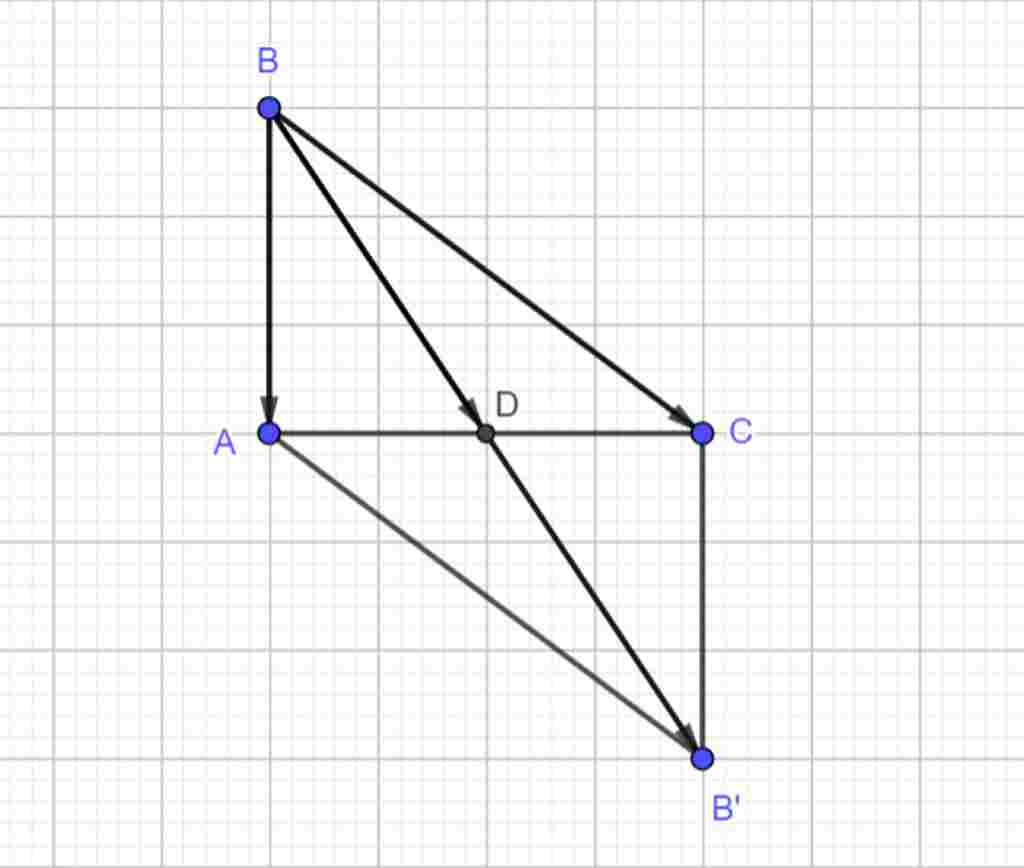
Gọi $D$ là trung điểm của $AC, B’$ đối xứng với $B$ qua $M$, $AD=\dfrac{AC}2=\dfrac42=2$
$\Rightarrow ABCB’$ là hình bình hành (tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
$\vec{CB}+\vec{AB}=-(\vec{BC}+\vec{BA})$
$=-\vec{BB’}$ (quy tắc hình bình hành)
$=-2\vec{BD}$
$\Rightarrow |\vec{CB}+\vec{AB}|=|-2\vec{BD}|=2BD$
Áp dụng định lý Pitago vào $\Delta ABD\bot A$
$BD^2=AB^2+AD^2=362+2^2=13$
$\Rightarrow BD=\sqrt{13}$
$\Rightarrow |\vec{CB}+\vec{AB}|=2BD=2\sqrt{13}$
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
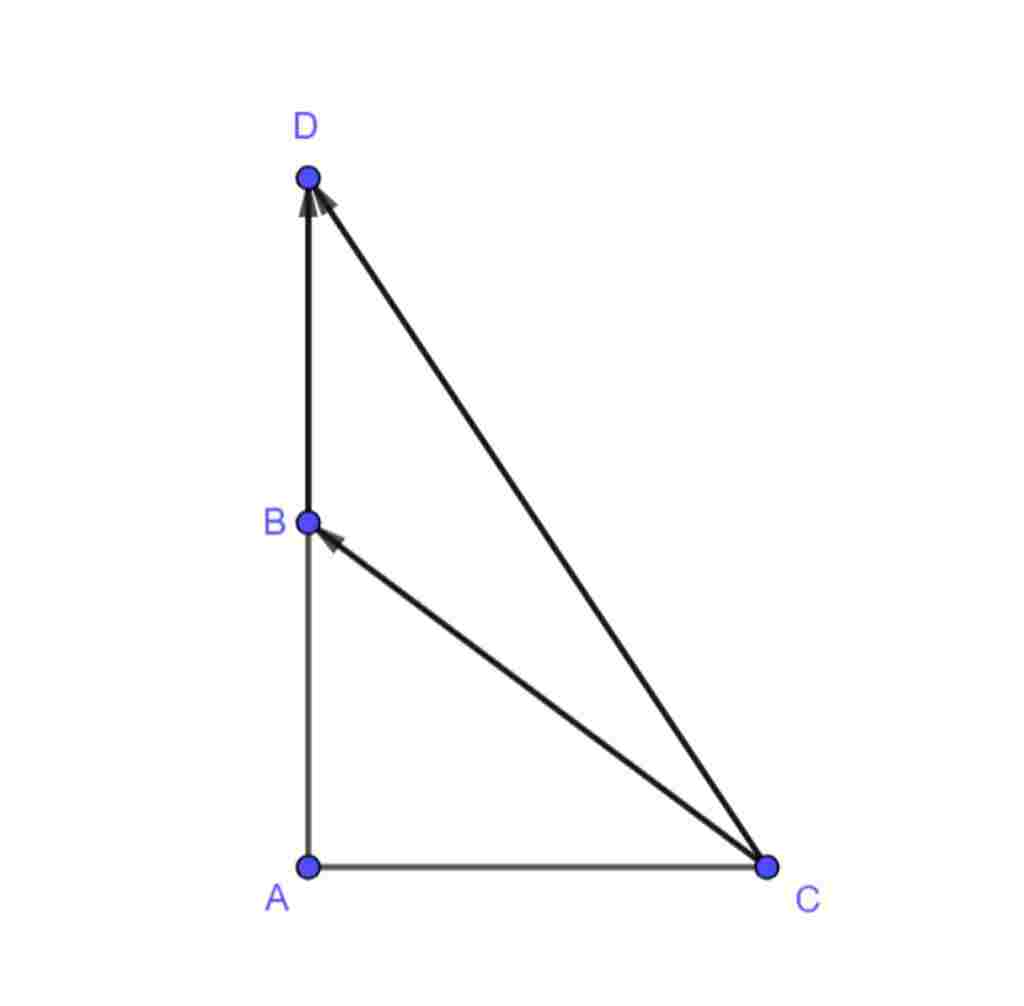
Trên tia đối của tia $BA$ lấy điểm $D$ sao cho $BA = BD$
$\Rightarrow \overrightarrow{AB} = \overrightarrow{BD}$
Áp dụng định lý Pytago, ta được:
$CD^2 = AD^2 + AC^2$
$\Rightarrow CD = \sqrt{AD^2 + AC^2} = \sqrt{6^2 + 4^2} = 2\sqrt{13}$
Ta được:
$|\overrightarrow{CB} + \overrightarrow{AB}|$
$= |\overrightarrow{CB} + \overrightarrow{BD}|$
$= |\overrightarrow{CD}| = CD = 2\sqrt{13}$